😅 插入排序

插入排序

有序性

有序通常分为非递增和非递减，递增一般是指严格的递增，即后一个元素必须比前一个元素大，不允许相等，而非递增指后一个元素必须比前一个元素小，允许相等，非递减同理

稳定性

排序的稳定性是指当前关键字相等时，排序前后的位置变化,在C++标准库中泛型算法为我们提供了容器的排序算法，sort为不稳定排序，stable_sort为稳定排序

//main1.cpp
array<int, 10> m_array;
for (int i = 0; i < 10; i++)
{
    m_array[i] = 10 - i;
}
printArray(m_array); // 10 9 8 7 6 5 4 3 2 1
sort(m_array.begin(), m_array.end(), [](const int &a, const int &b) -> bool
     { return (a < b); });
printArray(m_array); // 1 2 3 4 5 6 7 8 9 10
//稳定排序
stable_sort(m_array.begin(), m_array.end(), [](const int &a, const int &b) -> bool{ return (a > b); });
printArray(m_array); // 10 9 8 7 6 5 4 3 2 1

内部排序和外部排序

内部排序是数据在内存中进行排序，外部排序是因排序的数据很大，内存不能一次容纳全部数据，在排序过程中需要访问外存

直接插入排序

1、算法思想
直接插入排序是最简单的排序方法，每次将一个待排序的记录，插入到已经排好序的数据序列中，得到一个新的长度增1的有序表

2、算法步骤

设待排序的记录存储在数组r[1..n]中，可以把第一个记录r[1]看作一个有序序列。
依次将r[i](i=2,…,n)插入到已经排好序的序列r[1…i-1],并保持有序性。

3、代码实现

//main2.cpp
//直接插入排序 升序
void straightInsertSort(int array[], int n)
{
    //从下标1处理到下标n
    for (int i = 1; i <= n; i++)
    {
        //寻找插入位置
        int j = i - 1;
        int val = array[i];
        while (j >= 0 && array[j] > val)
        {
            array[j + 1] = array[j];
            cout << "[" << i << "] " << array[0] << " " << array[1] << " " << array[2] << " " << array[3] << " " << array[4] << endl;
            j--;
        }
        if (i - 1 != j) //原来array[i]需要进行移动
        {
            array[++j] = val;
        }
    }
}

void printArray(int m_array[5])
{
    for (int i = 0; i < 5; i++)
    {
        cout << m_array[i] << " ";
    }
    cout << endl;
}

int main(int argc, char **argv)
{
    int array[] = {1, 3, 4, 2, 5};
    straightInsertSort(array, 4);
    printArray(array); // 1 2 3 4 5
    int array1[] = {5, 4, 3, 2, 1};
    straightInsertSort(array1, 4);
    printArray(array1); // 1 2 3 4 5
    return 0;
}

4、时间复杂度分析
直接插入排序根据排序序列的不同，找插入位置的时间复杂度是不同的，可分为最好、最坏、平均情况分析

最好情况，本身是正序的，每个记录只需要和前一个记录比较，不小于前一个记录，则什么都不做，总的比较次数为

最坏情况，待排序序列本身是逆序的，每个记录都要比较i次，包括前i-1记录比较，如(5,4,3,2,1)比较次数为(0,1,2,3,4)，等差数列求和

平均情况，若待排序序列出现的概率相等，则可取最好情况和最坏情况的平均值，为O(n^2)

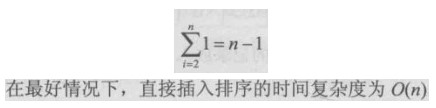
5、空间复杂度
常量空间，O(1)

6、稳定性
此算法是稳定的，但是与比较运算符息息相关，如在寻找插入位置时如果元素相等时还向前找，则变成了不稳定的排序算法

void straightInsertSort(int array[], int n)
{
    //从下标1处理到下标n
    for (int i = 1; i <= n; i++)
    {
        //寻找插入位置
        int j = i - 1;
        int val = array[i];
        while (j >= 0 && array[j] >= val)
        {
            array[j + 1] = array[j];
            cout << "[" << i << "] " << array[0] << " " << array[1] << " " << array[2] << " " << array[3] << " " << array[4] << endl;
            j--;
        }
        if (i - 1 != j) //原来array[i]需要进行移动
        {
            array[++j] = val;
        }
    }
}

折半插入排序

1、算法步骤

从前面的有序子表中查找出待插入元素应该被插入的位置（使用二分查找搜索待插入位置）
给插入位置腾出空间，将待插入元素填入

2、代码实现

//main3.cpp
void sort(vector<int> &vec)
{
    int low = 0, high, n = vec.size() - 1;
    //从第二个元素开始
    for (int i = 1; i <= n; i++)
    {
        low = 0, high = i - 1; //二分查找范围
        while (low <= high)
        {
            int mid = (low + high) / 2; //中间元素
            if (vec[mid] > vec[i])      //查找左子表
            {
                high = mid - 1;
            }
            else
            {
                low = mid + 1;
            }
        }
        // high+1位置即为要插入的位置
        int temp = vec[i];
        //将元素向后移动
        for (int j = i - 1; j >= high + 1; j--)
        {
            vec[j + 1] = vec[j];
        }
        vec[high + 1] = temp;
    }
}

int main(int argc, char **argv)
{
    vector<int> vec = {3, 4, 6, 2, 35, 6, 23, 6};
    printVec(vec); //[0]:3 [1]:4 [2]:6 [3]:2 [4]:35 [5]:6 [6]:23 [7]:6
    sort(vec);
    printVec(vec); //[0]:2 [1]:3 [2]:4 [3]:6 [4]:6 [5]:6 [6]:23 [7]:35
    return 0;
}

3、时间复杂度分析

二分查找复杂度为O(logn),一共进行n-1次二分查找，平均时间复杂度为O(nlogn),又需要移动位置平均时间复杂度为O(n^{2),故折半插入排序的平均平均时间复杂度为O(n}2)。

4、稳定性

折半插入排序是一种稳定的排序算法

希尔排序

希尔排序又称“缩小增量排序”，将待排序记录按下标的一定增量分组，对每组记录使用直接插入排序算法排序（达到基本有序），随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个序列基本有序，再对全部记录进行一次直接插入排序

1、算法步骤

设待排序的记录存储在数组r[1..n]中，增量序列为{d1,d2,…,dt},n>d1>d2>…>dt=1
第一趟取增量d1，所有间隔为d1的记录分别在一组，对每组记录进行直接插入排序
第二趟取增量d2，所有间隔为d2的记录分别在一组，对每组记录进行直接插入排序
一次进行下去，知道所取增量dt=1,所有记录在一组中进行直接插入排序

2、代码实现

#include <iostream>
#include <vector>
using namespace std;

// main4.cpp
/**
 * @brief 写入增量直接插入排序
 *
 * @param vec
 * @param dk
 */
void shellInsert(vector<int> &vec, int dk)
{
    for (int i = dk; i < vec.size(); i++) //按照分量dk划分序列的第二个元素开始
    {
        //与待排序序列前一个元素比较
        if (vec[i] < vec[i - dk]) //比前一个元素要小
        {
            int temp = vec[i]; //暂存元素
            //寻找待插入位置
            int j = i - dk; //前一个元素位置
            while (j >= 0 && vec[j] > temp)
            {
                vec[j + dk] = vec[j];
                j -= dk;
            }
            vec[j + dk] = temp;
        }
    }
}

/**
 * @brief 希尔排序
 *
 * @param vec 待排序序列
 * @param d 增量序列
 */
void shellSort(vector<int> &vec, vector<int> &d)
{
    for (int k = 0; k < d.size(); k++)
    {
        //按照增量为d[k]进行希尔插入排序
        shellInsert(vec, d[k]);
    }
}

template <typename T>
void printVec(const T &t)
{
    for (size_t i = 0; i < t.size(); i++)
    {
        cout << t[i] << " ";
    }
    cout << endl;
}

int main(int argc, char **argv)
{
    vector<int> vec = {6, 5, 4, 3, 2, 5, 6, 2, 5};
    vector<int> d = {5, 4, 3, 2, 1}; //增量
    printVec<vector<int>>(vec);
    // 6 5 4 3 2 5 6 2 5
    shellSort(vec, d);
    // sort(vec.begin(), vec.end());
    printVec<vector<int>>(vec);
    // 2 2 3 4 5 5 5 6 6
    return 0;
}

3、复杂度分析

空间效率
仅使用了常数个辅助单元，空间复杂度为O(1)
时间效率
时间复杂度依赖增量序列的函数，当n在某个特定范围时，希尔排序的时间复杂度约为O(n^{(1.3)),最坏时间复杂度为O(n}2)
稳定性
当相同的关键字划分不到同一个子表内时，可能会改变指向的相对次序，因此希尔排序是一种不稳定的排序方法
适用性
希尔排序仅适用于线性表为顺序表存储的情况