😍 折半查找

折半查找

算法步骤

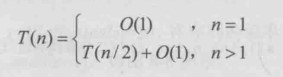
  1. 初始化。令low=0,即指向有序数组S[]的第一个元素；high=n-1,即指向有序数组S[]的最后一个元素
  2. 判定low<=high是否成立,如果成立则转向第3步，否则，算法结束
  3. middle=(low+high)/2.即指向查找范围的中间元素
  4. 判断x与S[middle]的关系，如果x==S[middle],则搜索成功，算法结束；如果x>S[middle],则令low=middle+1;否则令high=middle-1,转向第2步

代码实现

//main1.cpp
int find(vector<int>&vec,const int x){
    int low = 0, high = vec.size() - 1;
    while(low<=high){
        int middle = (low + high) / 2;//中间下标
        if(x==vec[middle]){
            return middle;
        }else if(x>vec[middle]){
            low = middle + 1;
        }else{
            high = middle - 1;
        }
    }
    return -1;
}

int main(int argc,char**argv){
    vector<int> vec = {1, 2, 3, 4, 5};
    cout << find(vec, 4) << endl;//3
    cout << find(vec, 9) << endl;//-1
    cout << find(vec, -2) << endl;//-1
    return 0;
}
//main2.cpp
//二分查找递归形式
int find(vector<int>&vec,const int x,const int low,const int high){
    if(low>high){
        return -1;
    }
    int middle = (low + high) / 2;
    if(x==vec[middle]){
        return middle;
    }else if(x<vec[middle]){
        return find(vec, x, low, middle - 1);
    }
    return find(vec, x, middle + 1, high);
}

int main(int argc,char**argv){
    vector<int> vec = {1, 2, 3, 4, 5, 6};
    vector<int> targets = {6, 5, 4, 3, 2, 1, 0, -2, 7};
    //5 4 3 2 1 0 -1 -1 -1
    for(auto&item:targets){
        cout << find(vec,item,0,vec.size()-1) << " ";
    }
    cout << endl;
    return 0;
}

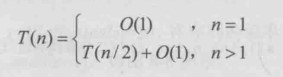
时间复杂度分析

时间复杂度
递归推导

空间复杂度分析

非递归算法，使用辅助变量是常数阶，因此空间复杂度为O(1)
递归算法则需要栈来实现

递归树

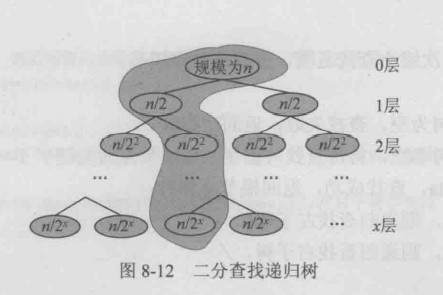
栈内每个上下文的空间复杂度为常数阶，则递归树的最大深度为logn,则空间复杂度为O(logn)