🥳 散列表

散列表

散列查找的精髓在于散列表的散列函数，线性表和树表的查找都是通过比较关键字的方法，查找的效率取决于关键字的比较次数，而散列表就是一种以不进行关键字比较为驱动目标的数据结构

散列函数

又称为哈希函数，将关键字映射到存储地址的函数，记作为hash(key)=Addr
（1）散列函数要尽可能简单，能够快速计算出任意一个关键字的散列地址
（2）散列函数映射的地址应该均匀分布整个地址空间，避免聚集，以减少冲突

直接定址法

散列函数 hash(key)=a*key+b
特点 使用于知道关键字、关键字集合不是很大但连续性很好，如果不连续则有大量空位，造成空间浪费

除留余数法

最常用的一种方法，不需要事先知道关键字的分布，假设散列表长度为m，去一个不大于表长的最大素数p

散列函数 hash(key)=key%p

为什么要选用素数？为了避免冲突

随机数法

随机可以让关键字的分布更均匀，再用除留余数法得到存储地址

散列函数 hash(key)=rand(key)%p

在C/C++中，rand(n)表示求0~n-1的随机树，p的取值和除留余数法相同

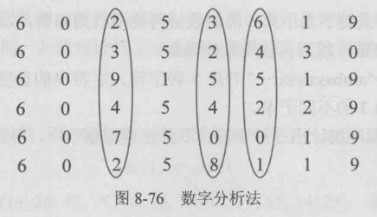
数字分析法

根据数字个别位上的分布进行具体问题具体分析

下面这些数字前1、2位相同，则不管，第3、5、6位分布较均匀，用这些位组成hash函数的key则会尽可能减少冲突

数字分析法

则可以将3、5、6位的数字作为散列地址，或将3、5、6位数字求和后作为散列地址等，真正要选择什么，还要看具体的使用场景

平方取中法

对关键字平方后，按散列表大小，取中间的若干位作为散列地址，通常适用于事先不知道关键字的分布且关键字的位数不是很大的情况

例：散列地址为3位

10123^2=102475129
//则在102475129中间取3位，作为关键字的10123的hash地址

折叠法

将关键字从左到右分割成位数相等的几部分，将这及部分叠加求和，取后几位作为散列地址
适用于关键字位数很多，事先不知道分布的情况

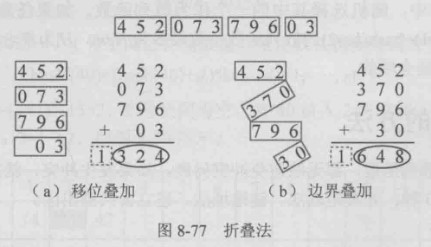
移位折叠法 分割后将每一个部分的最低位对齐，然后相加求和
边界折叠法 将相邻部分沿边界来回折叠，然后对齐相加

例：关键字为45207379603,散列地址为3位

折叠法

基数转换法

散列函数大多是基于整数的
十进制数转换为其他进制表示，例如345的九进制表示423
浮点数可将关键字乘以M并四舍五入得到整数，再进行散列函数,或将关键字表示为二进制数后在使用散列函数
字符可将字符转换R进制的整数，然后再使用散列函数

基数转换法应用举例

全域散列法

如果对关键字了解不多，可使用全域散列法
将备选的散列函数放入集合H,使用时随机取一个作为散列函数
如果任意两个不同的关键字key1!=key2,hash(key1)=hash(key2)的散列函数个数最多为|H|/m,|H|为集合中散列函数的个数,m为表长，则称H为全域的

处理冲突

什么是散列冲突，就是不同的关键字通过hash函数得到了相同的hash地址
无论如何设计散列函数，都无法避免冲突问题，只能减少冲突，主要有3种方法，开放地址法、链地址法、建立公共溢出区

开放地址法

hash'(key)=(hash(key)+di)%m

hash(key)为原散列函数，hash’(key)为探测函数，di为增量序列，m为表长

（1）线性探测法

例：一组关键字{14,36,42,38,40,15,19,12,51,65,34,25},表长为15，散列函数为hash(key)=key%13

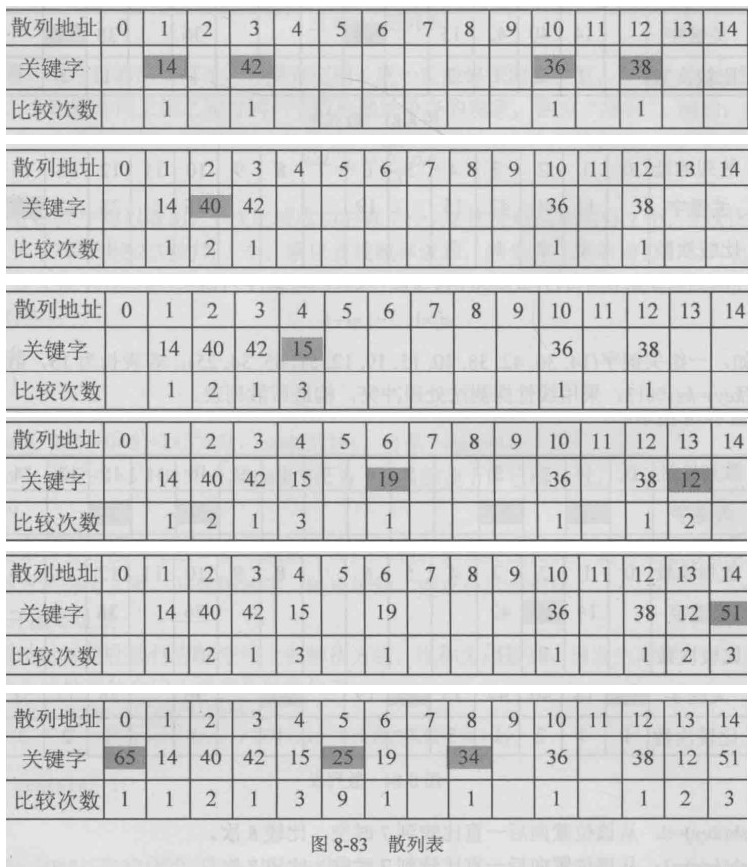
线性探测法

查找成功的平均查找长度等于所有关键字查找成功的比较次数ci乘以查找概率pi之和

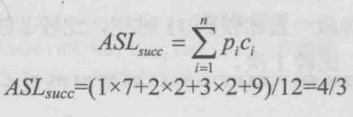
查找成功的平均查找长度
查找失败
查找失败的平均查找长度 
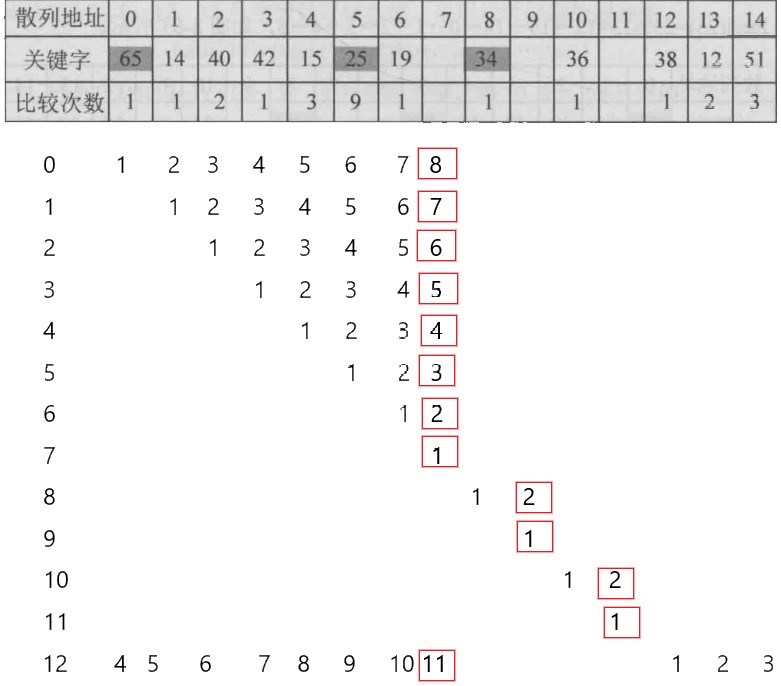
//main1.cpp
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;

#define m 15      //哈希表的表长
#define NULLKEY 0 //单元为空的标记

int HT[m], HC[m];

int H(int key) //哈希函数
{
    return key % 13;
}

//线性探测
int Linedetect(int HT[], int H0, int key, int &cnt)
{
    int Hi;
    for (int i = 1; i < m; ++i)
    {
        cnt++;
        Hi = (H0 + i) % m; //按照线性探测法计算下一个哈希地址Hi
        if (HT[Hi] == NULLKEY)//找到空的位置
            return Hi; //若单元Hi为空，则所查元素不存在
        else if (HT[Hi] == key)//找到目标关键字
            return Hi; //若单元Hi中元素的关键字为key
    }
    return -1;
}

//二次探测法
int Seconddetect(int HT[], int H0, int key, int &cnt)
{
    int Hi;
    for (int i = 1; i <= m / 2; ++i)
    {
        int i1 = i * i;
        int i2 = -i1;
        cnt++;
        Hi = (H0 + i1) % m;    //按照线性探测法计算下一个哈希地址Hi
        if (HT[Hi] == NULLKEY) //若单元Hi为空，则所查元素不存在
            return Hi;
        else if (HT[Hi] == key) //若单元Hi中元素的关键字为key
            return Hi;
        cnt++;
        Hi = (H0 + i2) % m; //按照线性探测法计算下一个哈希地址Hi
        if (Hi < 0)
            Hi += m;
        if (HT[Hi] == NULLKEY) //若单元Hi为空，则所查元素不存在
            return Hi;
        else if (HT[Hi] == key) //若单元Hi中元素的关键字为key
            return Hi;
    }
    return -1;
}

int SearchHash(int HT[], int key)
{
    //在哈希表HT中查找关键字为key的元素，若查找成功，返回哈希表的单元标号，否则返回-1
    int H0 = H(key); //根据哈希函数H（key）计算哈希地址
    int Hi, cnt = 1;
    if (HT[H0] == NULLKEY) //若单元H0为空，则所查元素不存在
        return -1;
    else if (HT[H0] == key) //若单元H0中元素的关键字为key，则查找成功
    {
        cout << "查找成功，比较次数：" << cnt << endl;
        return H0;
    }
    else
    {
        Hi = Linedetect(HT, H0, key, cnt);
        if (HT[Hi] == key) //若单元Hi中元素的关键字为key，则查找成功
        {
            cout << "查找成功，比较次数：" << cnt << endl;
            return Hi;
        }
        else
            return -1; //若单元Hi为空，则所查元素不存在
    }
}

bool InsertHash(int HT[], int key)
{
    int H0 = H(key); //根据哈希函数H（key）计算哈希地址
    int Hi = -1, cnt = 1;
    if (HT[H0] == NULLKEY) //不冲突
    {
        HC[H0] = 1;   //统计比较次数
        HT[H0] = key; //若单元H0为空，放入
        return 1;
    }
    else
    {
        Hi = Linedetect(HT, H0, key, cnt); //线性探测
        // Hi=Seconddetect(HT,H0,key,cnt);//二次探测
        if ((Hi != -1) && (HT[Hi] == NULLKEY)) //表不满
        {
            HC[Hi] = cnt;
            HT[Hi] = key; //若单元Hi为空，放入
            return 1;
        }
    }
    return 0;
}

void print(int HT[])
{
    for (int i = 0; i < m; i++)
        cout << HT[i] << "\t";
    cout << endl;
}

int main()
{
    int x;
    memset(HT, 0, sizeof(HT)); // hash表
    memset(HC, 0, sizeof(HC)); //存储判断次数
    print(HT);
    cout << "输入12个关键字，存入哈希表中：" << endl;
    for (int i = 0; i < 12; i++)
    {
        cin >> x; // 14 36 42 38 40 15 19 12 51 65 34 25
        if (!InsertHash(HT, x))
        {
            cout << "创建哈希表失败！" << endl;
            return 0;
        }
    }
    cout << "输出哈希表：" << endl;
    print(HT);
    print(HC);
    cout << "输入要查找的关键字" << endl;
    cin >> x;
    int result = SearchHash(HT, x);
    if (result != -1)
        cout << "在第" << result + 1 << "位置找到" << endl;
    else
        cout << "未找到" << endl;
    return 0;
}

（2） 二次探测

二次探测法采用前后跳跃式探测的方法，发生冲突时，向后1位探测，向前一位探测，向后22位探测，向前22位探测…

二次探测的增量序列为
di=1^2,-1^2,2^2,-2^2,...,k^2,-k^2(k<=m/2)

//二次探测法
int Seconddetect(int HT[], int H0, int key, int &cnt)
{
    int Hi;
    for (int i = 1; i <= m / 2; ++i)
    {
        int i1 = i * i;
        int i2 = -i1;
        cnt++;//向后探测
        Hi = (H0 + i1) % m;    //按照线性探测法计算下一个哈希地址Hi
        if (HT[Hi] == NULLKEY) //若单元Hi为空，则所查元素不存在
            return Hi;
        else if (HT[Hi] == key) //若单元Hi中元素的关键字为key
            return Hi;
        cnt++;//向前探测
        Hi = (H0 + i2) % m; //按照线性探测法计算下一个哈希地址Hi
        if (Hi < 0)
            Hi += m;
        if (HT[Hi] == NULLKEY) //若单元Hi为空，则所查元素不存在
            return Hi;
        else if (HT[Hi] == key) //若单元Hi中元素的关键字为key
            return Hi;
    }
    return -1;
}

缺点：二次探测法是跳跃式探测，效率较高，但是会出现明明有空间却探测不到的清苦那个，因而存储失败，而线性探测只要有空间就一定能够探测成功

（3）随机探测法

随机探测法采用伪随机数进行探测，利用随机化避免堆积，随机探测的增量序列为
di=伪随机序列

（4）再散列法

当通过散列函数得到的地址发生冲突时，再利用第二个散列函数处理，也称为双散列法
再散列法的增量序列为 di=hash2(key)

链地址法

像每个hash地址相同的关键字拉成一个链表，形成多个链表。链地址法又称为拉链法，查找、插入、删除操作主要在这个链表中进行，拉链法适用于经常进行插入、删除的情况

例：一组关键字{14,36,42,38,40,15,19,12,51,65,34,25},表长为15，散列函数为hash(key)=key%13

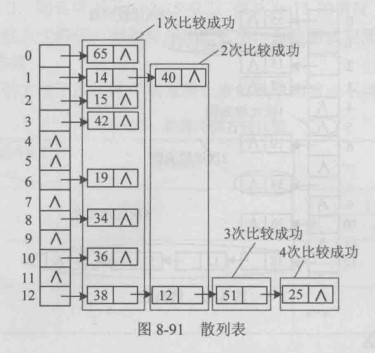
链地址法处理冲突

若每个关键字被查找的概率相同

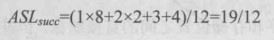
链地址法查找成功的平均查找长度
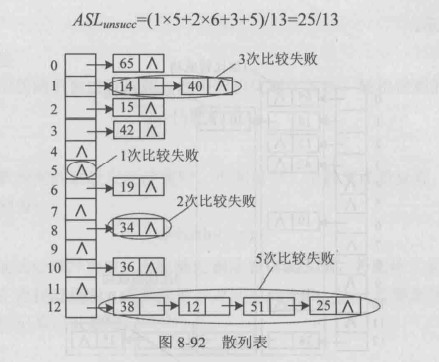
链地址法查找失败的平均查找失败

建立公共溢出区

建立一个公共溢出区，发生冲突时，关键字放入公共溢出区，查找时先根据关键字的散列地址在散列表查找，如果为空则查找失败，如果非空且不相等，则前往公共溢出区查找，如果仍未找到，则查找失败

散列函数

衡量散列函数好坏的标准是：简单、均匀。散列函数简单，可以将关键字均匀映射到散列表，其查找效率取决于3个因素，即散列函数、装填因子和处理冲突的方法

装填因子

装填因子a=(表中填入的记录数)/(散列表的长度)

装填因子反映散列表的装满程度，a越小，发生冲突的可能性越小，反之则相反，但是装填因子越小，也会造成空间浪费

处理冲突方法对比

散列表的平均查找长度与装填因子有关，与关键字个数无关

处理冲突方法比较

查找长度计算方法

查找长度计算方法