二叉查找树的性质
1、若左子树非空,则左子树上所有节点的值均小于根节点的值
2、若右子树非空,则右子树上所有节点的值均大于根节点的值
3、其左右子树本身又各是一棵二叉查找树
左子树<根<右子树,二叉查找树的中序遍历是一个递增序列
1、若二叉查找树为空,查找失败,返回空指针
2、若二叉查找树非空,将待查找关键字x与根节点的关键字T->data比较
//main1.cpp
BSTree SearchBST(BSTree T,ElemType key)//二叉排序树的递归查找
{
//若查找成功,则返回指向该数据元素结点的指针,否则返回空指针
if((!T)|| key==T->data)
return T;
else if (key<T->data)
return SearchBST(T->lchild,key);//在左子树中继续查找
else
return SearchBST(T->rchild,key); //在右子树中继续查找
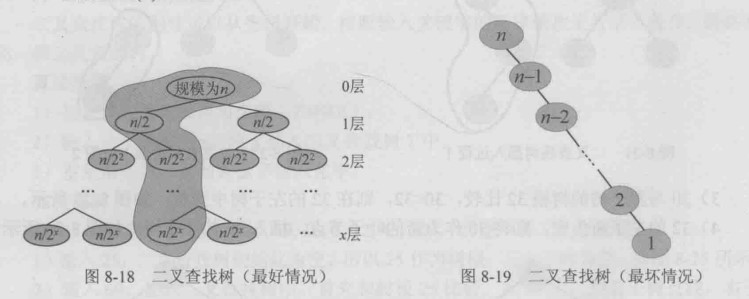
}最好情况的平均查找长度为)(logn) ,最坏情况的平均查找长度为O(n)

n各节点的二叉查找树有n!棵(形态不同)的二叉查找树,在平均情况下,二叉查找树的平均查找长度为O(logn)
空间复杂度为O(1)
1、若二叉查找树为空,创建一个新的节点s,将待插入关键字放入新节点的数据域,s节点作为根节点,左右子树均为空
2、若二叉查找树非空,将待查找关键字x与根节点的关键字T->data比较
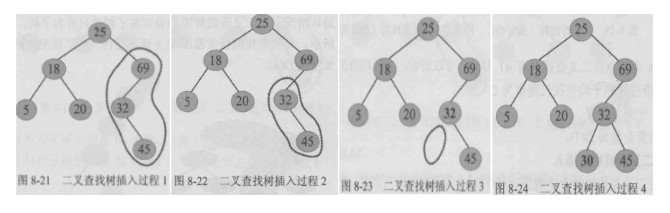
//main1.cpp
void InsertBST(BSTree &T,ElemType e)//二叉排序树的插入
{
//当二叉排序树T中不存在关键字等于e的数据元素时,则插入该元素
if(!T)
{
BSTree S=new BSTNode; //生成新结点
S->data=e; //新结点S的数据域置为e
S->lchild=S->rchild=NULL;//新结点S作为叶子结点
T=S; //把新结点S链接到已找到的插入位置
}
else if(e<T->data)
InsertBST(T->lchild,e );//插入左子树
else if(e>T->data)
InsertBST(T->rchild,e);//插入右子树
}查找插入位置复杂度为O(logn),插入本身为常数时间
1、初始化二叉查找树为空树,T=NULL
2、输入一个关键字x,将x插入二叉查找树T中
3、重复步骤2,直到关键字输入完毕
//main1.cpp
void CreateBST(BSTree &T )//二叉排序树的创建
{
//依次读入一个关键字为key的结点,将此结点插入二叉排序树T中
T=NULL;
ElemType e;
cin>>e;
while(e!=ENDFLAG)//ENDFLAG为自定义常量,作为输入结束标志
{
InsertBST(T,e); //插入二叉排序树T中
cin>>e;
}
}共n此插入,每次平均时间复杂度为O(logn),则总的平均时间复杂度为O(nlongn),实际的时间复杂度与二叉查找树的形状相关,与选中的基准元素有关
有三种情况
1、被删除节点左子树为空
右子树继承父业
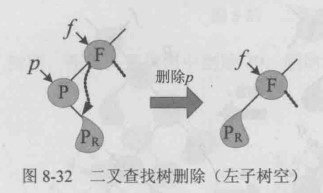
2、被删除节点右子树为空
左子树继承父业
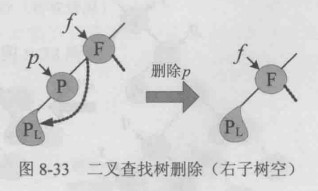
3、被删除节点左子树右子树均不空
需要利用直接前驱或者直接后继替代其位置
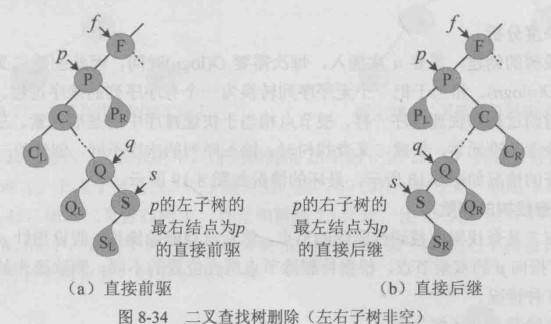
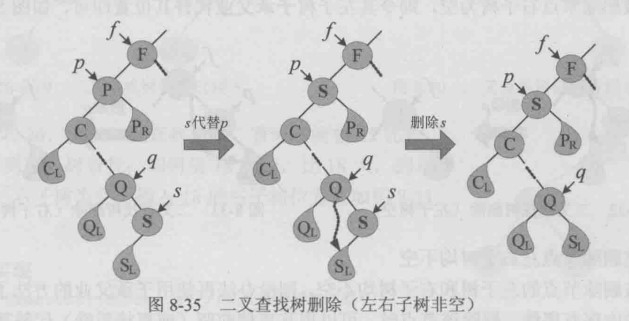
利用直接直接前驱进行调整
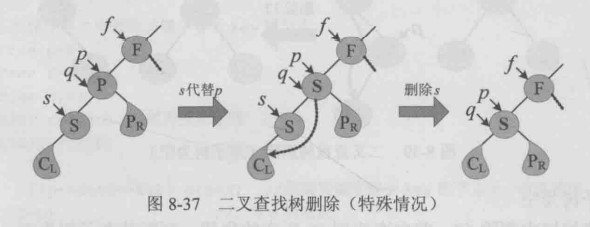
直接前驱的特殊情况为其直接前驱为其左孩子时
//main1.cpp
void DeleteBST(BSTree &T,char key)
{
//从二叉排序树T中删除关键字等于key的结点
BSTree p=T;BSTree f=NULL;
BSTree q;
BSTree s;
if(!T) return; //树为空则返回
while(p)//查找目标节点且记录其双亲节点
{
if(p->data==key) break; //找到关键字等于key的结点p,结束循环
f=p; //f为p的双亲
if (p->data>key)
p=p->lchild; //在p的左子树中继续查找
else
p=p->rchild; //在p的右子树中继续查找
}
if(!p) return; //找不到被删结点则返回
//三种情况:p左右子树均不空、无右子树、无左子树
if((p->lchild)&&(p->rchild))//被删结点p左右子树均不空
{
q=p;
s=p->lchild;
while(s->rchild)//在p的左子树中继续查找其前驱结点,即最右下结点,直到器右孩子为空
{
q=s;//q为s的双亲节点
s=s->rchild;
}
//s为p的直接前驱节点
p->data=s->data; //s的值赋值给被删结点p,然后删除s结点
if(q!=p)//q为s的双亲节点 直接前驱不是其左孩子
q->rchild=s->lchild; //重接q的右子树 直接前驱节点被其左子树替代
else
q->lchild=s->lchild; //重接q的左子树
delete s;
}
else
{
if(!p->rchild)//被删结点p无右子树,只需重接其左子树
{
q=p;//q为需要接到p的位置
p=p->lchild;
}
else if(!p->lchild)//被删结点p无左子树,只需重接其右子树
{
q=p;//q需要接到p的位置
p=p->rchild;
}
//将p所指的子树挂接到其双亲结点f相应的位置
if(!f)//被删结点为根结点
T=p;
else if(q==f->lchild)
f->lchild=p; //挂接到f的左子树位置
else
f->rchild=p;//挂接到f的右子树位置
delete q;
}
}查找目标节点时间需要O(logn)时间,如果需要查找被删节点你的前驱或者后继也需要O(logn)时间,二叉查找树的删除时间复杂度为O(logn)