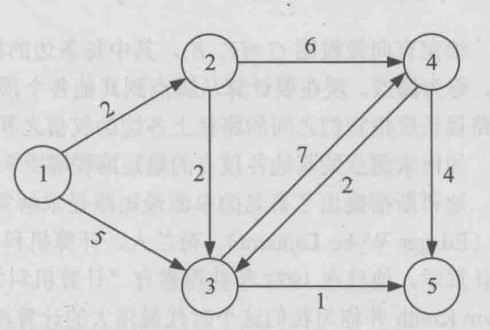
Dijkstra算法是解决单源最短路径问题的贪心算法,它先求出长度最短的一条路径,再参照该路径求出长度次短的一条路径,直到求出从源点到其他各个顶点的最短路径
算法步骤
1、数据结构设置地图的带权邻接矩阵G.Edge[j],即如果从源点u到i有边就令G.Edge[u][i]等于<u,i>的权值,则G.Edge[u][i]=∞,采用一位数组dist[i]来记录从源点到i顶点的最短路径长度,采用一维数组p[i]来记录最短路径上i顶点的前驱
2、初始化令集合S={u},对于集合V-S中的所有顶点x,初始化dist[i]=G.Edge[u][i],如果源点u到顶点i右边相连,初始化p[i]=u,否则p[i]=-1
3、找最小在集合V-S中依照贪心策略来寻找使得dist[j]具有最小值的顶点t,即dist[t]=min(dist[j]j属于V-S集合),则顶点t就是集合V-S中距离源点u最近的顶点
3、加入S战队将顶点t加入集合S中,同时更新V-S
4、判结束如果集合V-S为空,算法结束
5、借东风在第3步中已经找到了源点到t的最短路径,那么对集合V-S中所有与顶点t相邻的顶点j,都可以借助t走捷径,如果dist[j]>dist[t]+G.Edge[t][j],则dist[j]=dist[t]+G.Edge[t][j],记录顶点j的前驱为t,有p[j]=t,转到第3步
样例步骤

1 2 3 4 5
∞ 2 5 ∞ ∞ dist[] 0 2 5 ∞ ∞
∞ ∞ 2 6 ∞
∞ ∞ ∞ 7 1 1 2 3 4 5
∞ ∞ 2 ∞ 4 p[] -1 1 1 -1 -1
∞ ∞ ∞ ∞ ∞ V-S={2,3,4,5}
dist[2]最小,入战队V-S={2,3,4,5} 借东风
1 2 3 4 5
∞ 2 5 ∞ ∞ dist[] 0 2 4 8 ∞
∞ ∞ 2 6 ∞
∞ ∞ ∞ 7 1 1 2 3 4 5
∞ ∞ 2 ∞ 4 p[] -1 1 2 2 -1
∞ ∞ ∞ ∞ ∞ V-S={3,4,5}
dist[3]最小,入战队V-S={4,5} 借东风
1 2 3 4 5
∞ 2 5 ∞ ∞ dist[] 0 2 4 8 4
∞ ∞ 2 6 ∞
∞ ∞ ∞ 7 1 1 2 3 4 5
∞ ∞ 2 ∞ 4 p[] -1 1 2 2 3
∞ ∞ ∞ ∞ ∞ V-S={4,5}
dist[4]最小,入战队V-S={5} 借东风
1 2 3 4 5
∞ 2 5 ∞ ∞ dist[] 0 2 4 8 4
∞ ∞ 2 6 ∞
∞ ∞ ∞ 7 1 1 2 3 4 5
∞ ∞ 2 ∞ 4 p[] -1 1 2 2 3
∞ ∞ ∞ ∞ ∞ V-S={5}
dist[5]最小,如战队V-S={} 结束算法代码实现
//main1.cpp
#include<iostream>
#include <cstring>
#include <stack>
#include <climits>
using namespace std;
const int MaxVnum = 100; // 城市的个数可修改
const int INF = INT_MAX; // 无穷大10000000
int dist[MaxVnum], p[MaxVnum]; //最短距离和前驱数组
bool flag[MaxVnum]; //如果s[i]等于true,说明顶点i已经加入到集合S;否则顶点i属于集合V-S
typedef string VexType; //顶点的数据类型,根据需要定义
typedef int EdgeType; //边上权值的数据类型,若不带权值的图,则为0或1
typedef struct
{
VexType Vex[MaxVnum];//顶点
EdgeType Edge[MaxVnum][MaxVnum];
int vexnum, edgenum; //顶点数,边数
} AMGragh;
//根据顶点数据x找到相应顶点的下标
int locatevex(AMGragh G, VexType x)
{
for (int i = 0; i < G.vexnum; i++) //查找顶点信息的下标
if (x == G.Vex[i])
return i;
return -1; //没找到
}
//初始化邻接矩阵
void CreateAMGraph(AMGragh &G)
{
int i, j, w;
VexType u, v;
cout << "请输入顶点数:" << endl;
cin >> G.vexnum;
cout << "请输入边数:" << endl;
cin >> G.edgenum;
cout << "请输入顶点信息:" << endl;
for (int i = 0; i < G.vexnum; i++) //输入顶点信息,存入顶点信息数组
cin >> G.Vex[i];
for (int i = 0; i < G.vexnum; i++) //初始化邻接矩阵为无穷大
for (int j = 0; j < G.vexnum; j++)
G.Edge[i][j] = INF;
cout << "请输入每条边依附的两个顶点及权值:" << endl;
while (G.edgenum--)
{
cin >> u >> v >> w;
i = locatevex(G, u); //查找顶点u的存储下标
j = locatevex(G, v); //查找顶点v的存储下标
if (i != -1 && j != -1)
G.Edge[i][j] = w; //有向图邻接矩阵
else
{
cout << "输入顶点信息错!请重新输入!" << endl;
G.edgenum++; //本次输入不算
}
}
}
//单源最短路径算法
void Dijkstra(AMGragh G, int u)
{
for (int i = 0; i < G.vexnum; i++)
{
dist[i] = G.Edge[u][i]; //初始化源点u到其他各个顶点的最短路径长度
flag[i] = false;
if (dist[i] == INF)
p[i] = -1; //源点u到该顶点的路径长度为无穷大,说明顶点i与源点u不相邻
else
p[i] = u; //说明顶点i与源点u相邻,设置顶点i的前驱p[i]=u
}
dist[u] = 0;
flag[u] = true; //初始时,集合S中只有一个元素:源点u true代表加入到S
for (int i = 0; i < G.vexnum; i++)
{
int temp = INF, t = u;
for (int j = 0; j < G.vexnum; j++) //在集合V-S中寻找距离源点u最近的顶点t
if (!flag[j] && dist[j] < temp)
{
t = j;
temp = dist[j];
}
if (t == u)
return; //找不到t,则也代表V-S为空跳出循环
flag[t] = true; //否则,将t加入集合
for (int j = 0; j < G.vexnum; j++) //更新与t相邻接的顶点到源点u的距离
if (!flag[j] && G.Edge[t][j] < INF)//为临时顶点的出度
if (dist[j] > (dist[t] + G.Edge[t][j]))
{
dist[j] = dist[t] + G.Edge[t][j];//借东风
p[j] = t;//更改前驱
}
}
}
//根据前驱数组寻找路径
void findpath(AMGragh G, VexType u)
{
int x;
stack<int> S;
cout << "源点为:" << u << endl;
for (int i = 0; i < G.vexnum; i++)//找起点到每个顶点的最短路径
{
x = p[i];//目标顶点的前驱
if (x == -1 && u != G.Vex[i])
{
cout << "源点到其它各顶点最短路径为:" << u << "--" << G.Vex[i] << " sorry,无路可达" << endl;
continue;
}
while (x != -1)
{
S.push(x);//入栈
x = p[x];//向前找前驱
}
cout << "源点到其它各顶点最短路径为:";
while (!S.empty())//弹出最短路径
{
cout << G.Vex[S.top()] << "--";
S.pop();
}
cout << G.Vex[i] << " 最短距离为:" << dist[i] << endl;
}
}
int main()
{
AMGragh G; //邻接矩阵存储图
int st;
VexType u;
CreateAMGraph(G); //初始化图信息
cout << "请输入源点的信息:" << endl;
cin >> u;
st = locatevex(G, u); //查找源点u的存储下标
Dijkstra(G, st); //单源最短路径算法
cout << "小明所在的位置:" << u << endl;
for (int i = 0; i < G.vexnum; i++)
{
cout << "小明:" << u << " - "
<< "要去的位置:" << G.Vex[i];
if (dist[i] == INF)
cout << "sorry,无路可达" << endl;
else
cout << "最短距离为:" << dist[i] << endl;
}
findpath(G, u); //根据前驱数组找最短路径
return 0;
}算法复杂度分析
时间复杂度 O(n^2)
空间复杂度 O(n)
Floyd算法可以求解任意两个顶点的最短路径,Floyd算法又称插心法,其算法核心是在顶点i到顶点j之间,插入顶点k,看是否能够缩短i和j之间的距离(松弛操作)
算法步骤
1、数据结构设置地图的带权邻接矩阵G.Edge[j],即如果从i到j有边就令G.Edge[i][i]等于<i,j>的权值,则G.Edge[i][j]=∞,采用数组dist[i][j]来记录从i顶点到顶点j的最短路径长度,采用数组p[i][j]来记录从i到j顶点的最短路径上i顶点的前驱
2、初始化初始化dist[i][j]=G.Edge[i][j],如果顶点i到顶点j有边相连,初始化p[i][j]=i,否则p[i][j]=-1
3、插点,其实就是在i与j之间插入顶点k,看是否能够缩短i和j之间的距离,如果dist[i][j]>dist[i][k]+dist[k][j],则dist[i][j]=dist[i][k]+dist[k][j],记录i,j的前驱为p[i][j]=p[k][j]
代码实现
//main2.cpp
#include<iostream>
#include<cstring>
#include<climits>
using namespace std;
#define MaxVnum 100 //顶点数最大值
const int INF=INT_MAX; // 无穷大10000000
typedef string VexType; //顶点的数据类型,根据需要定义
typedef int EdgeType; //边上权值的数据类型,若不带权值的图,则为0或1
typedef struct{
VexType Vex[MaxVnum];
EdgeType Edge[MaxVnum][MaxVnum];
int vexnum,edgenum; //顶点数,边数
}AMGragh;
int dist[MaxVnum][MaxVnum],p[MaxVnum][MaxVnum];
int locatevex(AMGragh G,VexType x)
{
for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
if(x==G.Vex[i])
return i;
return -1;//没找到
}
void CreateAMGraph(AMGragh &G)//创建无向图的邻接矩阵
{
int i,j,w;
VexType u,v;
cout<<"请输入顶点数:"<<endl;
cin>>G.vexnum;
cout<<"请输入边数:"<<endl;
cin>>G.edgenum;
cout<<"请输入顶点信息:"<<endl;
for(int i=0;i<G.vexnum;i++)//输入顶点信息,存入顶点信息数组
cin>>G.Vex[i];
for(int i=0;i<G.vexnum;i++)//初始化邻接矩阵所有值为0,若是网,则初始化为无穷大
for(int j=0;j<G.vexnum;j++)
if(i!=j)
G.Edge[i][j]=INF;
else
G.Edge[i][j]=0; //注意i==j时,设置为0
cout<<"请输入每条边依附的两个顶点及权值:"<<endl;
while(G.edgenum--)
{
cin>>u>>v>>w;
i=locatevex(G,u);//查找顶点u的存储下标
j=locatevex(G,v);//查找顶点v的存储下标
if(i!=-1&&j!=-1)
G.Edge[i][j]=w; //有向图邻接矩阵存储权值
}
}
//用Floyd算法求有向网G中各对顶点i和j之间的最短路径
void Floyd(AMGragh G)
{
int i,j,k;
//各对结点之间初始已知路径及距离
for(i=0;i<G.vexnum;i++){
for(j=0;j<G.vexnum;j++)
{
dist[i][j]=G.Edge[i][j];
if(dist[i][j]<INF && i!=j)
p[i][j]=i; //如果i和j之间有弧,则将j的前驱置为i
else p[i][j]=-1; //如果i和j之间无弧,则将j的前驱置为-1
}
}
for(k=0;k<G.vexnum; k++)//插点
for(i=0;i<G.vexnum; i++)//i
for(j=0;j<G.vexnum; j++)//j
//从i经k到j的一条路径更短
if(dist[i][k]!=INF&&dist[k][j]!=INF&&dist[i][k]+dist[k][j]<dist[i][j])
{
dist[i][j]=dist[i][k]+dist[k][j]; //更新dist[i][j]
p[i][j]=p[k][j]; //更改j的前驱为k
}
}
void print(AMGragh G)
{
int i,j;
for(i=0;i<G.vexnum;i++)//输出最短距离数组
{
for(j=0;j<G.vexnum;j++)
cout<<dist[i][j]<<"\t";
cout<<endl;
}
cout<<endl;
for(i=0;i<G.vexnum;i++)//输出前驱数组
{
for(j=0;j<G.vexnum;j++)
cout<<p[i][j]<<"\t";
cout<<endl;
}
}
//递归形式,同理也是利用栈的性质,逆推且正向输出
void DisplayPath(AMGragh G,int s,int t )//显示最短路径
{
if(p[s][t]!=-1)
{
DisplayPath(G,s,p[s][t]);
cout<<G.Vex[p[s][t]]<<"-->";
}
}
int main()
{
VexType start,destination;
int u,v;
AMGragh G;
CreateAMGraph(G);
Floyd(G);
print(G);
cout<<"请依次输入路径的起点与终点的名称:";
cin>>start>>destination;
u=locatevex(G,start);
v=locatevex(G,destination);
DisplayPath(G,u,v);
cout<<G.Vex[v]<<endl;
cout<<"最短路径的长度为:"<<dist[u][v]<<endl;
cout<<endl;
return 0;
}算法复杂度分析
时间复杂度O(n^3),Floyd是一个暴力枚举的算法,尝试了尽有的可能,保留最优的
空间复杂度O(n^2)
Dijkstra算法无法处理带负权值边的图,Floyd算法可以处理带负权值边的图,但是不允许图中包含负圈(权值为负的圈),其他解决负权值边的最短路径算法Bellman-Ford和SPFA算法