🚲 图的存储与基本操作

图的存储与基本操作

邻接矩阵

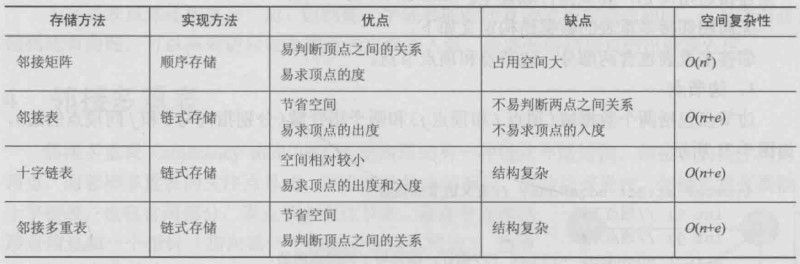
        |1，若(vi,vj)∈E
M[i][j]=|
        |0,其他

无向图邻接矩阵的特点

1、无向图的邻接矩阵是一个对称矩阵，并且唯一
2、第i行或第i列非零元素的个数正好是第i个顶点的度

        |1，若<vi,vj>∈E
M[i][j]=|
        |0,其他

有向图邻接矩阵的特点

1、有向图的邻接矩阵不一定是对称的
2、第i行非零元素的个数正好是第i个顶点的出度，第i列非零元素的个数正好是第i个顶点的入度

网是带权的图，需要存储边的权值，则邻接矩阵表示为

        |wij,若(vi,vj)∈E或<vi,vj>∈E
M[i][j]=|
        |∞,其他（无穷表达不可达）
vexnum
3
edgenum
3
input vex info
0 1 2
input (i,j) format: i j
0 1
0 2
1 2
[
0 1 1 
1 0 1 
1 1 0 
]

样例代码

//main1.cpp
#include <iostream>
using namespace std;
#define MaxVnum 100   //顶点最大值
typedef char VexType; //顶点存储数据类型
using EdgeType = int; //权值数据类型

using AMGragh = class
{
public:
    VexType Vex[MaxVnum];
    EdgeType Edge[MaxVnum][MaxVnum];
    int vexnum, edgenum; //顶点数，边数
    void print();
    void CreateAMGraph();
};

void AMGragh::print()
{
    cout << "[\n";
    for (int i = 0; i < vexnum; i++)
    {
        for (int j = 0; j < vexnum; j++)
        {
            cout << Edge[i][j] << " ";
        }
        cout << endl;
    }
    cout << "]\n";
}

/**
 * @brief 创建无向图的邻接矩阵
 *
 * @param G
 */
void AMGragh::CreateAMGraph()
{
    AMGragh &G = *this;
    VexType u, v;
    cout << "vexnum" << endl;
    cin >> G.vexnum; //输入顶点数量
    cout << "edgenum" << endl;
    cin >> G.edgenum; //输入边数量
    cout << "input vex info" << endl;
    for (int i = 0; i < G.vexnum; i++)
    {
        cin >> G.Vex[i]; //输入顶点存储数据
    }
    //初始化邻接矩阵所有值为0
    for (int i = 0; i < G.vexnum; i++)
    {
        for (int j = 0; j < G.vexnum; j++)
        {
            G.Edge[i][j] = 0;
        }
    }
    cout << "input (i,j) format: i j" << endl;
    while (G.edgenum--)
    {
        int i, j;
        cin >> i >> j;
        if (i >= 0 && j >= 0)
        {
            G.Edge[i][j] = G.Edge[j][i] = 1;
        }
    }
}

int main(int argc, char **argv)
{
    AMGragh g;
    g.CreateAMGraph();
    g.print();
    return 0;
}

邻接矩阵的优点

邻接矩阵的缺点

邻接矩阵是图的数组表示法，还有一种边集数组表示法，每个边存储其起点与终点，如果是网，则增加一个权值域

struct Edge{
    int u;
    int v;
    int w;
};
Edge graph[100];//如100个边的图

边集数组存储方式计算顶点的度或查找边时都要遍历整个边集数组，时间复杂度为O(e),e为边的个数

邻接表法

无向图 
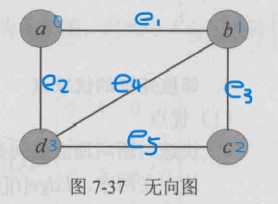
(0,3) (0,1) (1,2) (1,3) (2,3)
    data    first
0   a         ---> 3|next--->1|^
1   b         ---> 3|next--->2|next--->0|^//链长度为1的度数
2   c         ---> 3|next--->1|^
3   d         ---> 2|next--->1|next--->0|^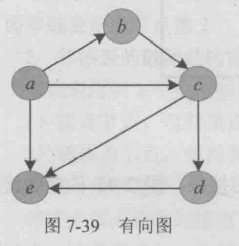
有向图 
<0,4> <0,2> <0,1> <1,2> <2,4> <2,3> <3,4>
    data    first
0   a         ---> 4|next--->2|next--->1|^
1   b         ---> 2|^//链长度为1的出度数
2   c         ---> 4|next--->3|^
3   d         ---> 4|^
4   e         ^
<0,4> <0,2> <0,1> <1,2> <2,4> <2,3> <3,4>
    data    first
0   a         ^
1   b         ---> 0|^
2   c         ---> 0|next--->1|^
3   d         ---> 2|^
4   e         ---> 0|next--->2|next-->3|^//链的长度为4的入度

代码实现

//main2.cpp
#include <iostream> //创建有向图的邻接表
using namespace std;
const int MaxVnum = 100; //顶点数最大值

typedef char VexType; //顶点的数据类型为字符型
typedef struct AdjNode
{                         //定义邻接点类型
    int v;                //邻接点下标
    struct AdjNode *next; //指向下一个邻接点
} AdjNode;

typedef struct VexNode
{                   //定义顶点类型
    VexType data;   // VexType为顶点的数据类型，根据需要定义
    AdjNode *first; //指向第一个邻接点
} VexNode;

typedef struct
{ //定义邻接表类型
    VexNode Vex[MaxVnum];
    int vexnum, edgenum; //顶点数，边数
} ALGragh;

//根据顶点数据找到顶点存储下标
int locatevex(ALGragh G, VexType x)
{
    for (int i = 0; i < G.vexnum; i++) //查找顶点信息的下标
        if (x == G.Vex[i].data)
            return i;
    return -1; //没找到
}

void insertedge(ALGragh &G, int i, int j) //插入一条边
{
    AdjNode *s;
    s = new AdjNode;
    s->v = j;
    s->next = G.Vex[i].first; //头插法
    G.Vex[i].first = s;
}

void printg(ALGragh G) //输出邻接表
{
    cout << "----------邻接表如下：----------" << endl;
    for (int i = 0; i < G.vexnum; i++)
    {
        AdjNode *t = G.Vex[i].first;
        cout << G.Vex[i].data << "：  ";
        while (t != NULL)
        {
            cout << "[" << t->v << "]  ";
            t = t->next;
        }
        cout << endl;
    }
}

void CreateALGraph(ALGragh &G) //创建有向图邻接表
{
    int i, j;
    VexType u, v;
    cout << "请输入顶点数和边数:" << endl;
    cin >> G.vexnum >> G.edgenum;
    cout << "请输入顶点信息:" << endl;
    for (i = 0; i < G.vexnum; i++) //输入顶点信息，存入顶点信息数组
        cin >> G.Vex[i].data;
    for (i = 0; i < G.vexnum; i++)
        G.Vex[i].first = NULL;
    cout << "请依次输入每条边的两个顶点u,v" << endl;
    while (G.edgenum--)
    {
        cin >> u >> v;
        i = locatevex(G, u); //查找顶点u的存储下标
        j = locatevex(G, v); //查找顶点v的存储下标
        if (i != -1 && j != -1)
            insertedge(G, i, j);
        else
        {
            cout << "输入顶点信息错！请重新输入！" << endl;
            G.edgenum++; //本次输入不算
        }
    }
}

int main()
{
    ALGragh G;
    CreateALGraph(G); //创建有向图邻接表
    printg(G);        //输出邻接表
    return 0;
}

邻接表的优点

1、便于访问所有邻接点，访问所有顶点的邻接点，时间复杂度为O(n+e)
2、空间复杂度低，顶点表占用n个空间，无向图的邻接点表占用n+2e个空间，有向图的邻接点表占用n+e个空间，总体空间复杂度为O(n+e),而邻接矩阵的空间复杂度为O(n^2)
3、便于增删节点

邻接表的缺点

1、不便于判断两顶点之间是否有边，要判断两顶点是否有边，需要遍历该顶点后面的邻接点链表
2、不便于计算各顶点的度，在无向图邻接表中，顶点的度为该顶点后面单链表中的节点数目，在有向图邻接表中，顶点的出度为该顶点后面单链表中的节点数，但求入度比较难。在有向图逆邻接表中，顶点的入度为该顶点后面单链表中的节点数，但求出度有困难

十字链表

十字链表

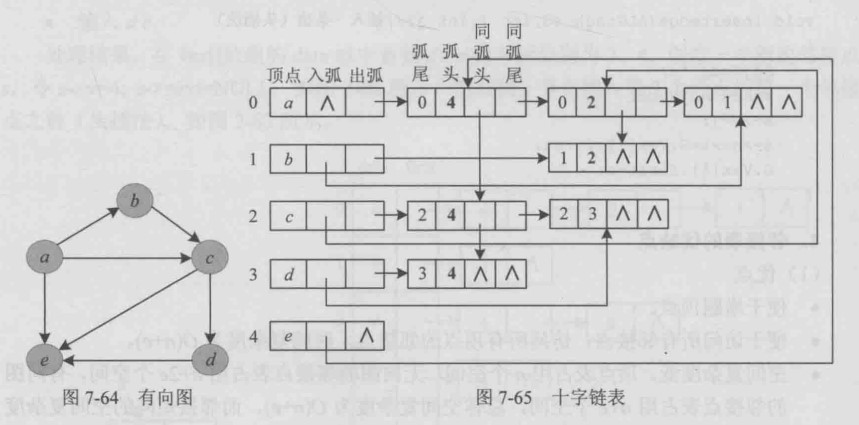
弧节点类型

typedef struct arcNode{
    int tail;//弧尾下标
    int head;//弧头下标
    struct arcNode *hlink;//指向同弧头节点
    struct arcNode *tlink;//指向同弧尾的弧
}arcNode;

顶点节点

typedef struct vexNode{
    VexType data;
    arcNode*firstin;//指向第一个入弧
    arcNode*firstout;//指向第一个出弧
}

十字链表结构

typedef struct{
    VexNode Vex[100];
    int vexnum,edgenum;//顶点数，边数
}

十字链表虽然结构复杂，但创建十字链表的时间复杂度和邻接表相同，十字链表存储有向图，可以高效访问每个顶带你的出弧和入弧，很容易得到顶点的出度和入度。

邻接多重表

邻接多重表是无向图的另一种链式存储结构，邻接表关注的是顶点，而邻接多重表关注的是边

无向图

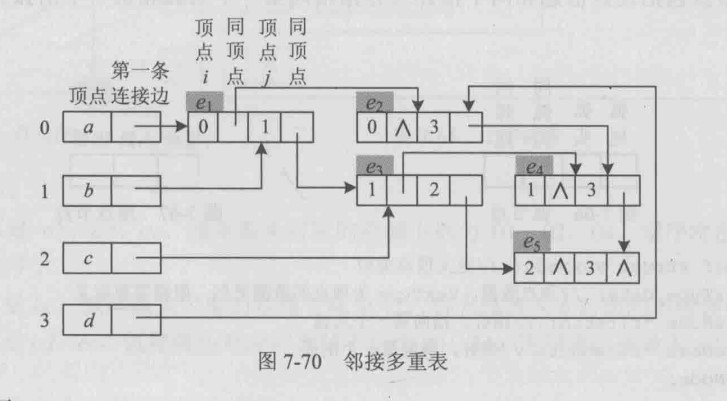
邻接多重表结构

邻接多重表

边节点

struct edgeNode{
    int i;//顶点下标
    int j;//顶点下标
    struct edgeNode*ilink;//指向与i同顶点的边
    struct edgeNode*jlink;//指向与j同顶点的边
};

顶点节点

struct vexNode{
    VexType data;
    edgeNode* firstedge;//指向第一条连接边
}

多重表结构

typedef struct{
    VexNode Vex[MaxVnum];
    int vexnum,edgenum;
}AMLGraph;

4种存储方法特点

4种存储方法的特点