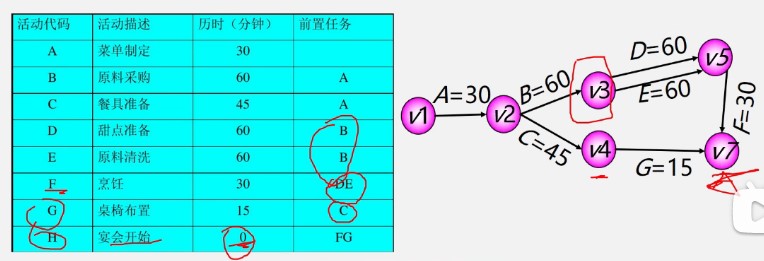
AOE
在有一堆有先后制约的任务,每个任务需要使用一定的时间完成

AOE
四个描述量
ve(vj)–表示事件vj的最早发生时间 ve(v1)=0 ve(v2)=30
vl(vj)–表示事件vj最迟发生事件 vl(v4)=165
e(i) –表示活动ai的最早开始时间 e(C)=30
l(i)–表示活动ai的最迟开始时间 l(C)=120
l(i)-e(i)–表示完成活动ai的时间余量
关键活动–关键路径上的活动,l(i)==e(i)的活动
weight
vi—->vj
e=ve[i] ; l=vl[j]-weight ;
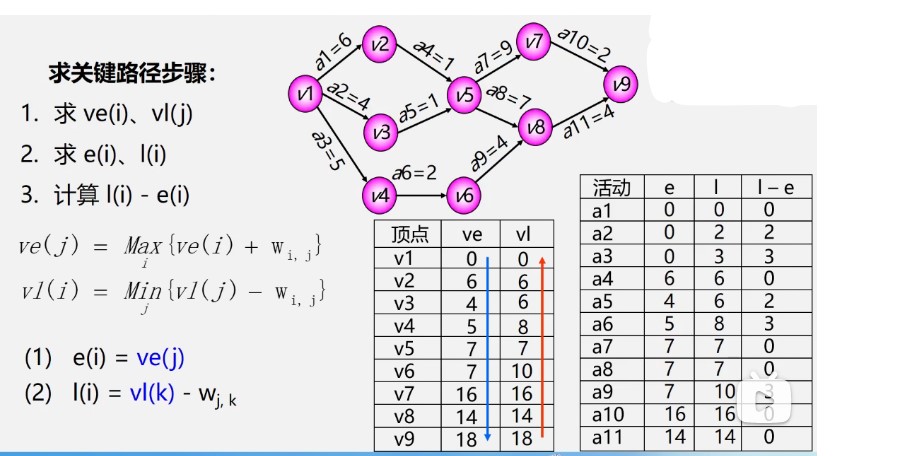
1、求ve(i)、vl(j)
2、求e(i)、l(i)
3、计算l(i)-e(i)
#include <iostream>
#include <cstring>
#include <stack>
using namespace std;
const int MaxVnum = 100; //顶点数最大值
int indegree[MaxVnum]; //入度数组
int ve[MaxVnum]; //事件vi的最早发生时间
int vl[MaxVnum]; //事件vi的最迟发生时间
typedef string VexType; //顶点的数据类型为字符型
typedef struct AdjNode
{ //定义邻接点类型
int v; //邻接点下标
int weight; //权值
struct AdjNode *next; //指向下一个邻接点指针
} AdjNode;
typedef struct VexNode
{ //定义顶点类型
VexType data; // VexType为顶点的数据类型,根据需要定义
AdjNode *first; //指向第一个邻接点指针
} VexNode;
typedef struct
{ //包含邻接表和逆邻接表
VexNode Vex[MaxVnum]; //定义邻接表
VexNode converse_Vex[MaxVnum]; //定义逆邻接表
int vexnum, edgenum; //顶点数,边数
} ALGragh;
int locatevex(ALGragh G, VexType x)
{
for (int i = 0; i < G.vexnum; i++) //查找顶点信息的下标
if (x == G.Vex[i].data)
return i;
return -1; //没找到
}
void insertedge(ALGragh &G, int i, int j, int w) //插入一条边
{
AdjNode *s1, *s2;
//创建邻接表结点
s1 = new AdjNode;
s1->v = j;
s1->weight = w;
s1->next = G.Vex[i].first;
G.Vex[i].first = s1;
//创建逆邻接表结点
s2 = new AdjNode;
s2->v = i;
s2->weight = w;
s2->next = G.converse_Vex[j].first;
G.converse_Vex[j].first = s2;
}
void printg(ALGragh G) //输出邻接表
{
cout << "----------邻接表如下:----------" << endl;
for (int i = 0; i < G.vexnum; i++)
{
AdjNode *t = G.Vex[i].first;
cout << G.Vex[i].data << ": ";
while (t != NULL)
{
cout << "[" << t->v << " " << t->weight << "] ";
t = t->next;
}
cout << endl;
}
cout << "----------逆邻接表如下:----------" << endl;
for (int i = 0; i < G.vexnum; i++)
{
AdjNode *t = G.converse_Vex[i].first;
cout << G.converse_Vex[i].data << ": ";
while (t != NULL)
{
cout << "[" << t->v << " " << t->weight << "] ";
t = t->next;
}
cout << endl;
}
}
void CreateALGraph(ALGragh &G) //创建有向图的邻接表和逆邻接表
{
int i, j, w;
VexType u, v;
cout << "请输入顶点数和边数:" << endl;
cin >> G.vexnum >> G.edgenum;
cout << "请输入顶点信息:" << endl;
for (i = 0; i < G.vexnum; i++) //输入顶点信息,存入顶点信息数组
{
cin >> G.Vex[i].data;
G.converse_Vex[i].data = G.Vex[i].data;
G.Vex[i].first = NULL;
G.converse_Vex[i].first = NULL;
}
cout << "请依次输入每条边的两个顶点及权值u,v,w" << endl;
while (G.edgenum--)
{
cin >> u >> v >> w;
i = locatevex(G, u); //查找顶点u的存储下标
j = locatevex(G, v); //查找顶点v的存储下标
if (i != -1 && j != -1)
insertedge(G, i, j, w);
else
{
cout << "输入顶点信息错!请重新输入!" << endl;
G.edgenum++; //本次输入不算
}
}
}
void FindInDegree(ALGragh G) //求出各顶点的入度存入数组indegree中
{
int i, count;
for (i = 0; i < G.vexnum; i++)
{
count = 0;
AdjNode *p = G.converse_Vex[i].first;
if (p)
{
while (p)
{
p = p->next;
count++;
}
}
indegree[i] = count;
}
cout << "入度数组为:" << endl;
for (int i = 0; i < G.vexnum; i++) //输出入度数组
cout << indegree[i] << "\t";
cout << endl;
}
bool TopologicalSort(ALGragh G, int topo[]) //拓扑排序
{
//有向图G采用邻接表存储结构
//若G无回路,则生成G的一个拓扑序列topo[]并返回true,否则false
int i, m;
stack<int> S; //初始化一个栈S,需要引入头文件#include<stack>
FindInDegree(G); //求出各顶点的入度存入数组indegree[]中
for (i = 0; i < G.vexnum; i++)
if (!indegree[i]) //入度为0者进栈
S.push(i);
m = 0; //对输出顶点计数,初始为0
while (!S.empty()) //栈S非空
{
i = S.top(); //取栈顶顶点i
S.pop(); //栈顶顶点i出栈
topo[m] = i; //将i保存在拓扑序列数组topo中
m++; //对输出顶点计数
AdjNode *p = G.Vex[i].first; // p指向i的第一个邻接点
while (p) // i的所有邻接点入度减1
{
int k = p->v; // k为i的邻接点
--indegree[k]; // i的每个邻接点的入度减1
if (indegree[k] == 0) //若入度减为0,则入栈
S.push(k);
p = p->next; // p指向顶点i下一个邻接结点
}
printg(G);
}
if (m < G.vexnum) //该有向图有回路
return false;
else
return true;
}
bool CriticalPath(ALGragh G, int topo[]) // G为邻接表存储的有向网,输出G的各项关键活动
{
int n, i, k, j, e, l;
if (TopologicalSort(G, topo))
{
cout << "拓扑序列为:" << endl;
for (int i = 0; i < G.vexnum; i++) //输出拓扑序列
cout << topo[i] << "\t";
cout << endl;
}
else
cout << "该图有环,无拓扑序列!" << endl;
n = G.vexnum; // n为顶点个数
for (i = 0; i < n; i++) //给每个事件的最早发生时间置初值0
ve[i] = 0;
//按拓扑次序求每个事件的最早发生时间
printg(G);
for (i = 0; i < n; i++)
{
k = topo[i]; //取得拓扑序列中的顶点序号k
AdjNode *p = G.Vex[k].first; // p指向k的第一个邻接顶点
while (p != NULL)
{ //依次更新k的所有邻接顶点的最早发生时间
j = p->v; // j为邻接顶点的序号
if (ve[j] < ve[k] + p->weight) //更新顶点j的最早发生时间ve[j]
ve[j] = ve[k] + p->weight;
p = p->next; // p指向k的下一个邻接顶点
}
}
for (i = 0; i < n; i++) //给每个事件的最迟发生时间置初值ve[n-1]
vl[i] = ve[n - 1];
//按逆拓扑次序求每个事件的最迟发生时间
for (i = n - 1; i >= 0; i--)
{
k = topo[i]; //取得逆拓扑序列中的顶点序号k
AdjNode *p = G.Vex[k].first; // p指向k的第一个邻接顶点
while (p != NULL)
{ //根据k的邻接点,更新k的最迟发生时间
j = p->v; // j为邻接顶点的序号
if (vl[k] > vl[j] - p->weight) //更新顶点k的最迟发生时间vl[k]
vl[k] = vl[j] - p->weight;
p = p->next; // p指向k的下一个邻接顶点
}
}
cout << "事件的最早发生时间和最迟发生时间:" << endl;
for (int i = 0; i < n; i++)
cout << ve[i] << "\t" << vl[i] << endl;
//判断每一活动是否为关键活动
cout << "关键活动路径权值之和为:" << vl[n - 1] << endl;
cout << endl;
cout << "关键活动路径为:";
for (i = 0; i < n; i++) //每次循环针对vi为活动开始点的所有活动
{
AdjNode *p = G.Vex[i].first; // p指向i的第一个邻接顶点
while (p != NULL)
{
j = p->v; // j为i的邻接顶点的序号
e = ve[i]; //计算活动<vi, vj>的最早开始时间e
l = vl[j] - p->weight; //计算活动<vi, vj>的最迟开始时间l
if (e == l) //若为关键活动,则输出<vi, vj>
cout << "<" << G.Vex[i].data << "," << G.Vex[j].data << "> ";
p = p->next; // p指向i的下一个邻接顶点
}
}
return true;
}
int main()
{
ALGragh G;
int *topo = new int[G.vexnum];
CreateALGraph(G); //创建有向图的邻接表和逆邻接表
printg(G); //输出邻接表和逆邻接表
CriticalPath(G, topo);
return 0;
}